8.- La sincronización
Hemos visto en anteriores artículos que es una función de transferencia y como podemos utilizar los filtros IIR para la corrección de un sistema. En éste, veremos que toda función de transferencia debe ser previamente sincronizada.
Recordemos algunos conceptos:
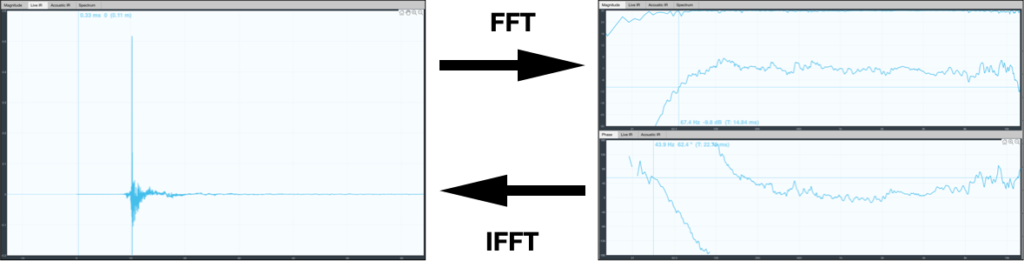
Como vimos en el artículo sobre la transformada de Fourier, la FFT es un algoritmo matemático que nos permite pasar del dominio del tiempo (impulso / forma de onda) al dominio de la frecuencia (Función de Transferencia / espectro de la señal) y que la transformada inversa (IFFT) del dominio de la frecuencia al dominio del tiempo.
También vimos que el ruido rosa, normalmente la señal de test utilizada en los analizadores clásicos, es una señal aleatoria que contiene la misma energía por octava.
Y que una función de Transferencia era básicamente comparar la señal que entra en un sistema respecto de su salida (realmente era aplicar una división)
Y qué tiene que ver todo esto con la sincronización?
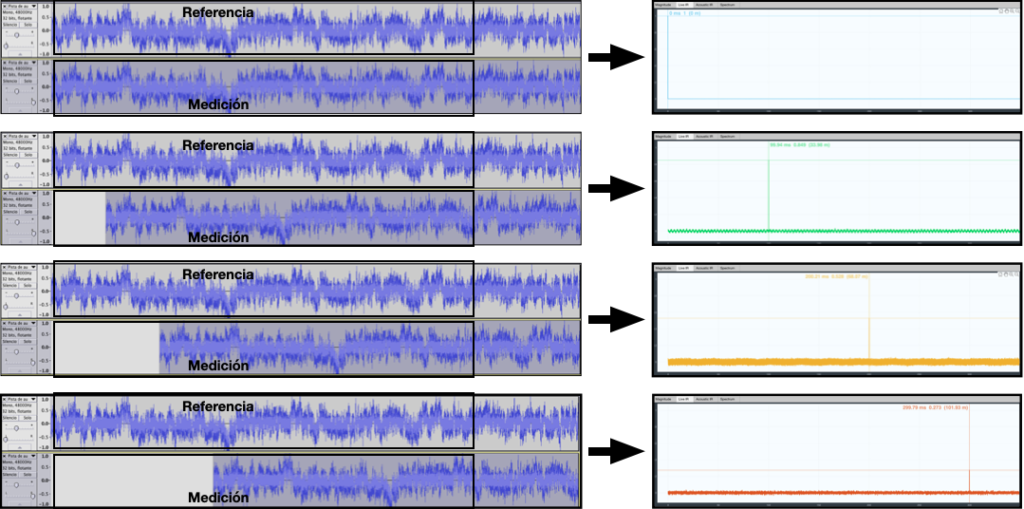
En una medición real, la señal de medición siempre se encontrará retrasada respecto de la señal de referencia.
Es decir, si comparamos la señal de referencia y de medición veremos que no comparten exactamente la misma información, ya que se encuentran en lugares distintos. El gráfico anterior muestra una función de transferencia no sincronizada.
Además, la señal de test que se ha venido utilizando habitualmente para el análisis es una señal aleatoria y esto implica que cuando la señal de medición está retrasada respecto de la señal de referencia parte de la señal obtenida no está presente en la señal generada y además está es desconocida para el analizador al ser aleatoria. Veremos que esto plantea algunos problemas.
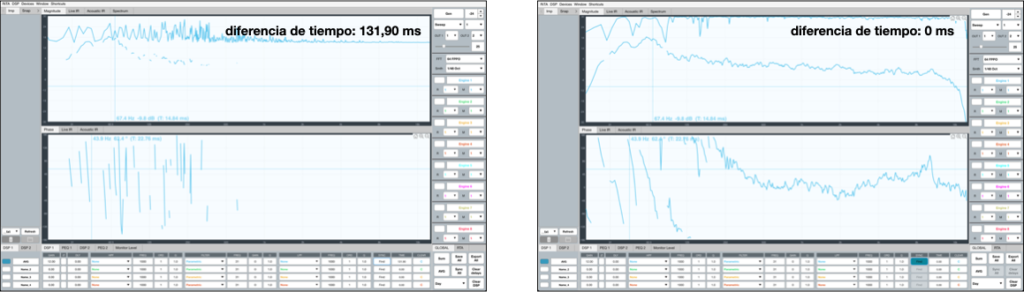
El siguiente gráfico muestra la misma medición sincronizada y sin sincronizar
Como vemos, sincronizar es colocar la señal de referencia y de medición en el mismo tiempo. De este modo garantizamos que la misma parte de excitación está presente en ambas señales.
Al sincronizar no solo estamos pudiendo visualizar correctamente el trazo de magnitud y fase sino también relacionar todos los altavoces que conforman nuestro diseño.
La sincronización nos servirá de posición ancla desde la cual vamos a observar las diferencias de tiempo entre nuestros sub-sistemas. Para conocer la diferencia de tiempo deberemos de estar sincronizados en algún lugar.
Supongamos un ejemplo donde queremos encontrar las diferencias de tiempo entre un sistema principal y un sistema de subgraves.
Nos encontramos con dos mediciones en distinto lugar respecto de la señal de referencia y que además no comparten las mismas frecuencias. Tendremos que sincronizar la referencia con una de las dos mediciones para poder conocer la diferencia de tiempo relativa a través del trazo de fase
Recordemos que el sistema clásico de medición consiste en excitar un sistema con una señal aleatoria y medir la respuesta de cada sistema a esa excitación.
Si sincronizamos la señal de referencia respecto del sistema principal, es decir, aplicamos a la señal de referencia un tiempo de delay para ponerla en el mismo lugar que la señal de medición, podremos analizar si la señal de medición del subgrave está adelantada o retrasada respecto de la señal de referencia, o lo que es lo mismo, saber si la señal del subgrave está adelantada o retrasada sobre el sistema principal
En caso contrario, lo veremos desde el punto del vista del subgrave. El altavoz principal llegará adelantado o retrasado respecto de la referencia, o lo que es lo mismo, adelantado o retrasado respecto del subgrave
La solución pasaba por aplicar 6,5 ms de delay al sistema principal, aunque también se podría haber solucionado aplicando un filtro APF.
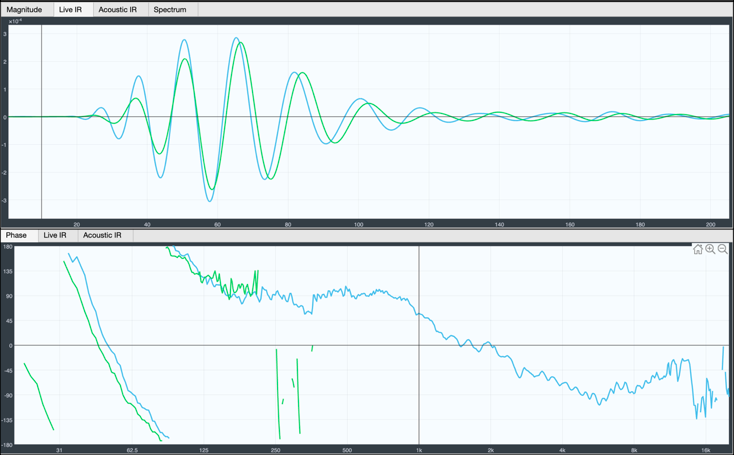
Podemos comprobar que las pendientes de fase están correctamente alineadas apoyándonos en la visualización del impulso de las frecuencias involucradas en el crossover acústico
Como vemos, la sincronización no es solamente útil para poder ver una función de transferencia sino también para relacionar en tiempo nuestros altavoces.
Ahora bien, como hace el analizador para conocer las diferencias de tiempo y poder sincronizarse?
Un posible método sería utilizar la correlación cruzada. En nuestro caso la autocorrelación (la correlación cruzada de una señal consigo mismo) entre la señal de medición y la señal de referencia.
Este método nos devuelve un pico de amplitud donde la máxima correlación ocurre y éste se verá desplazado el tiempo que las separa.
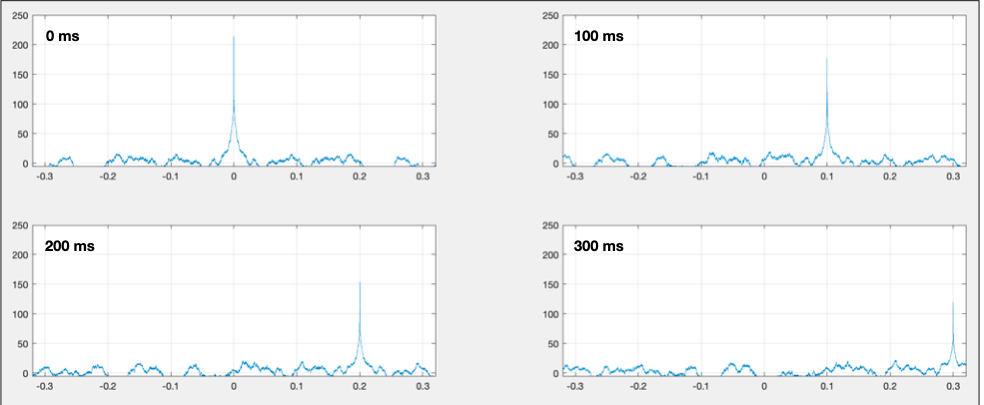
Veamos un ejemplo obteniendo la correlación cruzada de un ruido rosa consigo mismo y con diferentes tiempos de desplazamiento entre la señal de referencia y medición:
La muestra donde el pico ocurre nos indica la diferencia de tiempo que existe entre ambas señales.
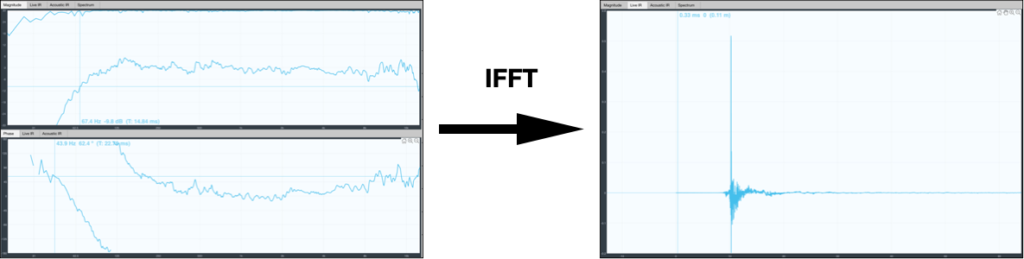
No obstante, este es un algoritmo que se calcula con las señales expresadas en el dominio del tiempo y los analizadores acostumbran a realizar los cálculos en el dominio de la frecuencia. Por lo que es común que utilicen la inversa de la transformada de Fourier (IFFT) para obtener el impulso que indique la diferencia de tiempo entre la referencia y la medición.
Es decir, el analizador obtiene una función de transferencia y sin sincronizar calcula la IFFT para localizar el tiempo. Este método acostumbra a llamarse find delay
El problema de esta técnica es que una función de trasferencia necesita siempre de estar sincronizada para poder comparar la misma parte de excitación en ambas señales. Y como hemos visto, a medida que la medición se aleja de la referencia cada vez menos parte de la referencia estará presente en la señal de medición.
Esta característica hace que la amplitud del impulso y la relación señal/ruido empeore considerablemente al alejarnos de la fuente y no sólo por la ley de la inversa al cuadrado.
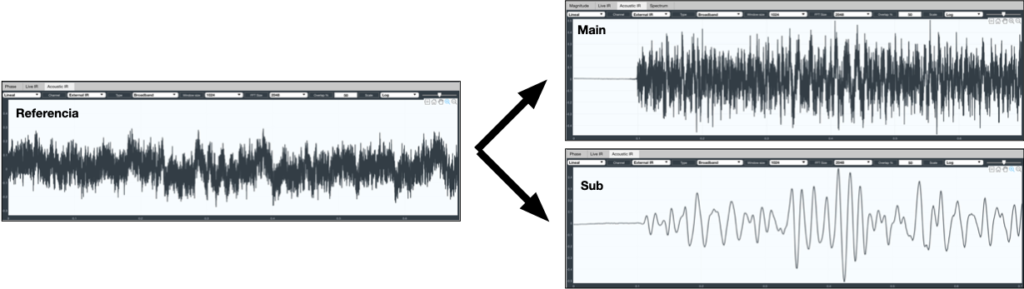
Veamos un ejemplo. Utilizaremos una señal aleatoria (ruido rosa) y la duplicaremos para simular una función de transferencia. A la señal de medición le iremos aplicando tiempos de retraso y calcularemos la respuesta al impulso en un analizador que utiliza este método.
Una vez obtenido el impulso lo importaremos para visualizar su resultado
Podemos observar, que a pesar de que estamos realizando una medición eléctrica, la amplitud del impulso decrece a medida que aumenta la distancia entre la referencia y la medición y además aumenta el ruido.
Este fenómeno es todavía más acusado en una medición real donde además nos encontraremos con una perdida de amplitud por la ley de la inversa al cuadrado. Veremos en otros artículos mejores técnicas para calcular respuestas al impulsos y detectar diferencias de tiempo.
En resumen, la sincronización es la herramienta que usaremos para relacionar las diferencias de tiempo entre nuestros altavoces y poder visualizar correctamente una función de transferencia








No Comments