4.- Optimización de Sistemas. La Función de Transferencia
Quién nunca ha entrado en una sala y ha generado una palmada? Casi de manera instintiva muchos técnicos e ingenieros de sonido realizamos este acto cuando entramos en el lugar que tendremos que sonorizar.
Fijaros que, de algún modo, lo que intentamos es generar un impulso d[n] con nuestro cuerpo que nos permita excitar el sistema (la sala) y obtener su respuesta al impulso h[n].
Y no solo eso, sin casi pensar en ello, somos capaces de, una vez escuchada la respuesta a la palmada (respuesta al impulso), pensar como sonará el sistema dentro de ese lugar.
Es decir, en el fondo nuestro cerebro es capaz de producir mentalmente una convolución, donde la salida del sistema y[n] será igual a la entrada del sistema x[n] convolucionada con la respuesta al impulso h[n].
Matemáticamente sabemos que cualquier sistema lineal e invariante en el tiempo queda unívocamente determinado por su respuesta al impulso. Y esta idea será la clave, como veremos en posteriores artículos, para obtener funciones de transferencia sin la necesidad de generar ruido de manera constante.
Bien, llegados a este punto, qué tiene que ver la palmada con una función de transferencia? y por qué realizar funciones de transferencia?
Si recordamos del anterior artículo, la Transformada de Fourier nos permite visualizar el contenido en frecuencia de una señal, pero nunca nos aporta información sobre la polaridad o el tiempo de la señal. Y, precisamente, la mayoría de problemas cuando configuramos un sistema de sonido son debidos a estos motivos.
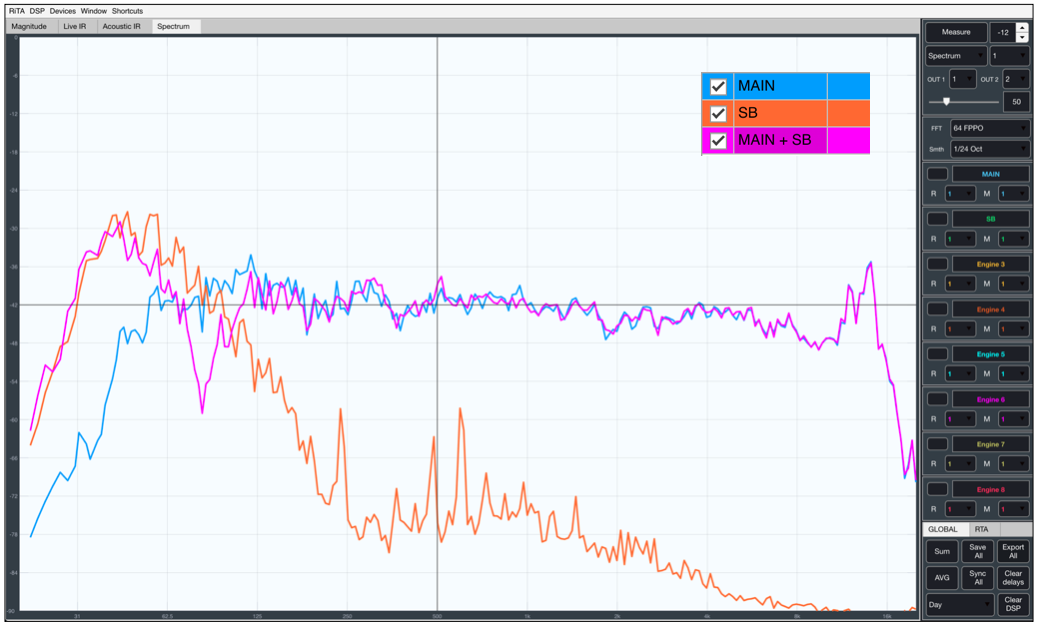
Fijémonos en el siguiente ejemplo: Un altavoz principal y un subgrave se encuentran con una diferencia de polaridad. Por lo que su combinación produce una cancelación en el crossover acústico. Y en ningún momento el gráfico de la respuesta espectral nos da información al respecto
A la pregunta de por qué realizar funciones de transferencia, la respuesta es simple, porque de algún modo necesitamos obtener información que nos permita no sólo visualizar la interferencia constructiva y destructiva sino determinar a través de la interpretación de los datos porque éstas se producen.
Y qué tiene que ver la palmada? Bien, revisemos un poco de teoría. El propio teorema de la convolución establece que una convolución en el dominio del tiempo es equivalente a una multiplicación en el dominio de la frecuencia.
Es decir, una convolución, algo menos eficaz computacionalmente, puede ser substituida por una multiplicación si las señales están expresadas en el dominio de la frecuencia. Y precisamente esto es lo que hace la transformada de Fourier, descomponer una señal temporal en sus componentes frecuenciales.
Una vez las señales han sido convertidas a frecuencia podemos volver a definir el ejemplo de la palmada como: la respuesta en frecuencia de la palmada a través de la sala tiene que ser igual a la respuesta en frecuencia de la palmada multiplicada por la respuesta en frecuencia de la sala.
Es decir, la respuesta de la sala (sistema) tiene que ser el cociente entre la salida del sistema (medición) y la entrada del sistema (Referencia). Simplemente despejamos la incógnita.
La señal de entrada al sistema es la señal que generamos, y la señal de salida del sistema es la que medimos.
Hasta ahora, hemos puesto el ejemplo de una sala, pero esta explicación es igual de valida para cualquier sistema lineal como lo es un altavoz.
Veamos en el siguiente gráfico el diagrama de bloques de una función de transferencia
Una función de transferencia es una medición de doble canal, donde necesitamos siempre una entrada y una salida del sistema y media sobre valores relativos.
Y como esta división es una división a complejos, obtendremos 2 respuestas, la estimación de la magnitud y la respuesta de fase.
La magnitud se obtiene como el módulo de la función de Transferencia y nos aporta información sobre el nivel y la frecuencia relativa. La respuesta de magnitud se suele representar de modo logarítmico como 20 veces el logaritmo en base 10 del módulo del valor obtenido.
la respuesta de fase nos aporta información sobre las diferencias de tiempo y el “retraso de grupo” relativo y se obtiene como la arcotangente del cociente entre el valor imaginario y real de la función de transferencia. Suele ser expresada en grados.
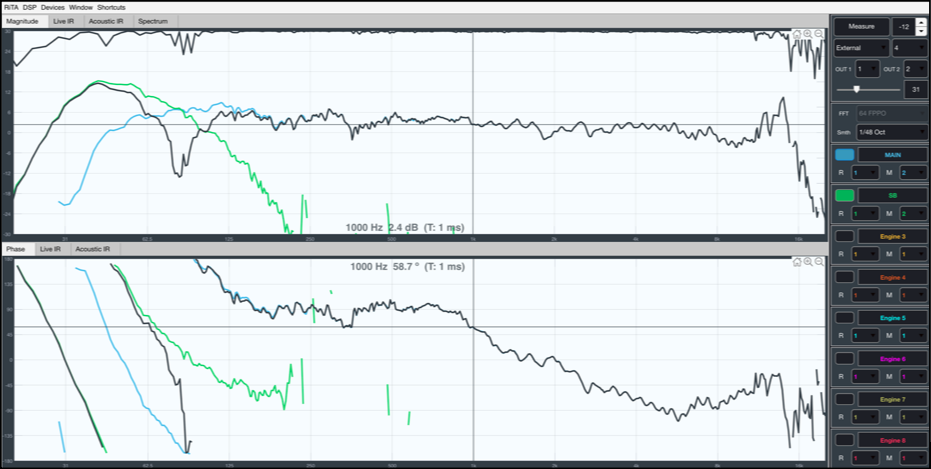
Si volvemos a visualizar el ejemplo anterior pero ahora desde el punto de vista de la función de trasferencia veremos que ahora sí podemos conocer porque se produce la cancelación. Una diferencia de polaridad, pendientes de fase paralelas.
Continuara…









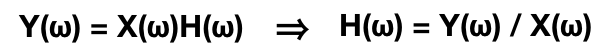


José Luis García
12 abril, 2023 at 12:39 amExelente 3xplicaciom pepe