3- Optimización de Sistemas. La Transformada de Fourier
Vimos en el primer artículo (fundamentos) como a través de la FFT podíamos visualizar el espectro de una señal expresada en el dominio del tiempo. Podríamos decir que la FFT descompone una señal en su contenido frecuencial (realmente obtiene las exponenciales complejas que están presentes en la señal)
Si bien en un primer momento el uso de analizadores RTA (Real Time Analyzer) basados en la obtención del espectro de la señal fue una ayuda para empezar a entender el comportamiento de los sistemas de sonido y a visualizar la interferencia constructiva y destructiva, rápidamente se encontraron sus limitaciones para el uso en la optimización de sistemas de sonido.
No obstante, todos los analizadores actuales destinados a la optimización de sistemas están basados de algún modo en la transformada rápida de Fourier
La respuesta espectral
La respuesta espectral de una señal es el funcionamiento más básico de un analizador y muestra su contenido en frecuencia.
Como veremos más adelante, esta técnica nos permite visualizar los problemas pero no nos da información de porque estos se producen.
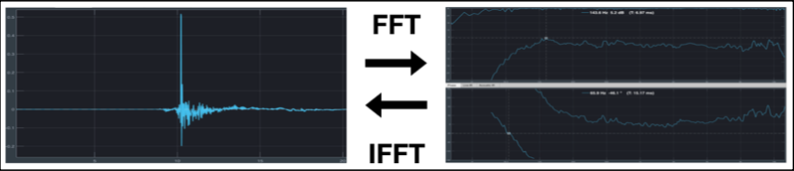
El siguiente gráfico nos muestra el diagrama de bloques del proceso para obtener la respuesta espectral
La integral de análisis X(ω) extrae la información espectral de una señal temporal
La integral de síntesis x[ t ] obtiene la señal temporal a partir de la información espectral
Realmente nuestro analizador usa la transformada Discreta de Fourier ya que manejamos señales discretas
Aunque existen técnicas mejores para la obtención de la respuesta al impulso, la IFFT es también usada en los analizadores clásicos para obtener el impulso a partir de una función de trasferencia
El tamaño de la FFT
Si nos fijamos en los analizadores actuales nos daremos cuenta de que todos los tamaños de FFT que podemos elegir son potencias de 2. Eso es debido a que usan el algoritmo de Cooley-Tukey para la transformada rápida.
Este algoritmo matemático nos permite, siempre y cuando el tamaño de la longitud de la señal (N) sea potencia 2 reducir los cálculos necesarios para obtener la transformada de N² a N log2 N.
Calculemos para 32768 muestras (2^15): 32768^2 = 1073741824 vs 32768 log2 32768 = 491520
Una diferencia de computación considerable.
El tamaño de la FFT determina 2 parámetros importantes: la Frecuencia de Resolución y la Constante de Tiempo (TC)
La Frecuencia de Resolución determina cuál es la mínima frecuencia que puede ser vista por el analizador. Todas las frecuencias que el analizador detectará son múltiplos enteros de esta Frecuencia de Resolución.
La Frecuencia de Resolución depende de la frecuencia de muestreo y del tamaño de la FFT
FR = Frecuencia de muestreo / Tamaño de la FFT
Ejemplo: 128 FFT y 32768 FFT
FR = 48000 / 128 = 375 Hz FR = 48000 / 32768 = 1,46 Hz
La frecuencia de resolución no es más que la frecuencia cuyo periodo coincide con la Constante de Tiempo
Aumentar la frecuencia de muestreo NO implica mejorar la resolución en frecuencia
La Constante de Tiempo es el tiempo necesario para capturar determinado número de muestras.
Como veremos mas adelante este valor es determinante para poder obtener un impulso mínimamente decente usando el método clásico (IFFT) para largas distancias, por ejemplo medir el sistema principal en una torre de delay.
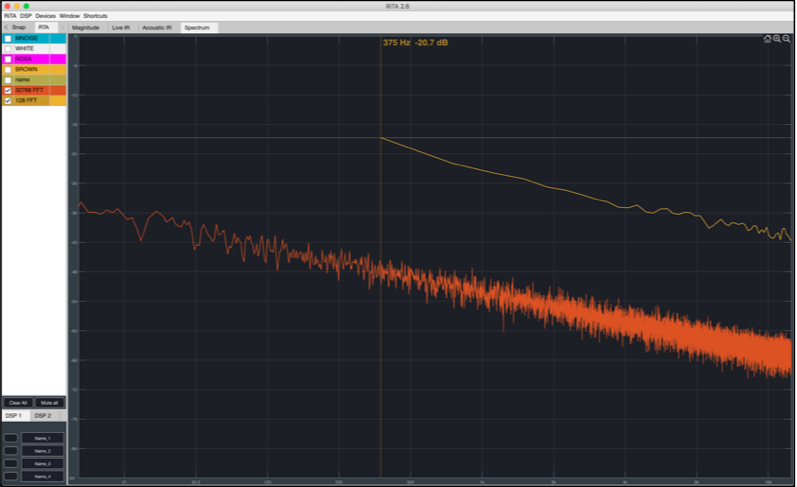
Sí visualizamos el espectro de una señal aleatoria con los tamaños de FFT mencionados anteriormente (32768 FFT, 128 FFT) Observaremos que nos muestran un resultado distinto. 32768 FFT tiene un dato cada 1,46 Hz, mientras que 128 FFT obtiene un dato cada 375 Hz. Además nos muestran una amplitud distinta (el software muestra la potencia de la señal convertida a dBFS
Entonces, ¿Qué tamaño de FFT deberíamos usar? Pues como casi siempre la respuesta es depende, depende de la frecuencia.
Un tamaño grande nos aportará buena resolución para las frecuencias graves, pero tantos datos para las frecuencias agudas que dificultarán su visualización, justo lo contrario que un tamaño pequeño.
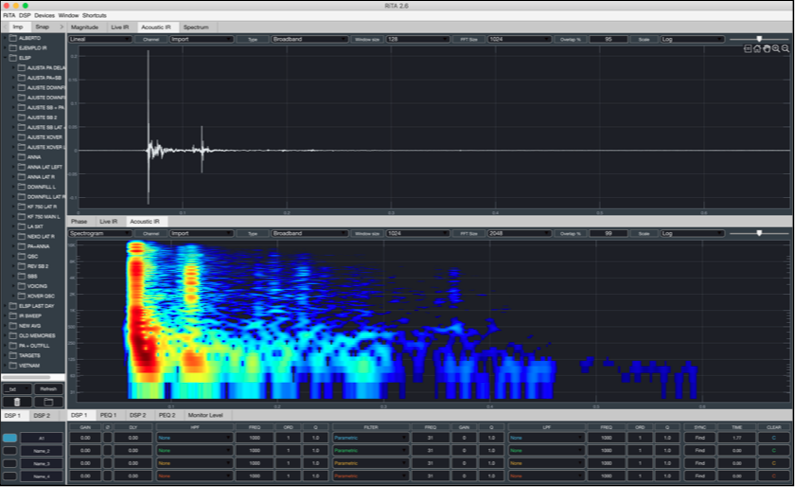
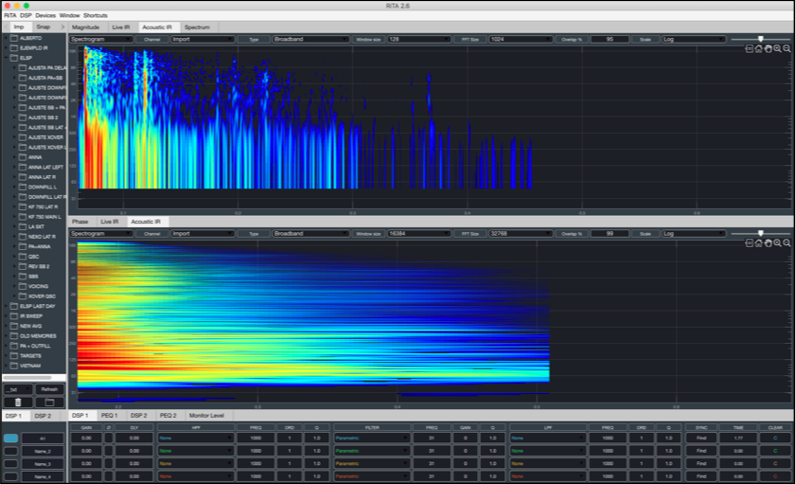
Veamos un nuevo ejemplo pero desde el punto de vista de la Constante de Tiempo. Visualicemos el espectrograma de una respuesta al impulso tomada en una sala.
Ambos gráficos nos muestran la misma respuesta al impulso pero con diferentes tamaños de FFT (realmente con diferente tamaño de ventana).
El gráfico superior (128 FFT) es capaz de mostrarnos una muy buena resolución temporal y, por lo tanto, mostrar claramente la reflexión que produce la pared trasera en una sala. Por contra, un tamaño grande de FFT nos muestra una buena resolución en frecuencia a cambio de no poder visualizar la reflexión ya que su constante de tiempo es demasiado grande.
Al final, como siempre, un valor intermedio puede mostrarnos un equilibrio entre ambos dominios










No Comments